
概念
什么是组合逻辑电路?
在任何时刻,电路的输出仅取决于该时刻的输入信号,而与电路原来的状态无关,这种电路称为组合逻辑电路。组合逻辑电路的特点
结构特点:电路只有从输入到输出的通路,没有从输出到输入的反馈回路。电路中不存在含有记忆功能的存储器件。
逻辑特点:只要输入量确定,那么各级的输出量皆可确定。
组合逻辑电路的分析与设计
组合逻辑电路的分析方法:
- 根据逻辑电路图,确定输入变量、输出变量、中间变量;
- 逐级推导出各输出端的逻辑函数表达式;
- 化简输出表达式,列出真值表;
- 根据输出表达式和真值表,概括逻辑功能。
组合逻辑电路的设计方法:
- 对问题进行逻辑抽象,列出真值表;
- 写出逻辑表达式;
- 化简逻辑表达式,并根据所需器件进行变换;
- 绘制逻辑电路图。
对于最简 与或 式,若需采用 与非 门实现,可以对该式两次取反,变换成 与非-与非 表达式;若需采用 或非 门实现,可以先转换成 或与 式(或者直接在卡诺图上圈0得到最简或与式),再两次取反,变换成 或非-或非 表达式。
当题目中有两组输出,且输入端共享,可以合理利用公共乘积项,以此优化电路设计。
例如:
可以利用公共乘积项,简化电路结构。
简化前(左/上)与简化后(右/下)电路结构对比:
 ⇨
⇨

如果选用 MSI 组合逻辑器件设计电路时,对于多输出函数来说,通常选用 译码器 实现电路较方便。对于单输出函数来说,选用 数据选择器 实现电路较方便。
常用中规模组合逻辑器件(MSI)包括加法器、编码器、译码器、数据选择器、数值比较器等,除了基本功能外,还要掌握这些器件的扩展和应用。
加法器
加法器是构成算术运算器的基本单元,两个二进制数之间所进行的算术运算加、减、乘、除等,在计算机中都是化作若干步加法运算进行的。实现1位加法运算的模块有半加器和全加器,实现多位加法运算的模块有串行进位加法器和超前进位加法器。
半加器
如果不考虑有来自低位的进位,将两个1位二进制数相加称为半加。半加器公式:
其中,A为被加数、B为加数,S为本位之和,CO为本位向高位的进位。
全加器
能对两个1位二进制数进行相加,并考虑低位来的进位,即相当于3个1位二进制数相加,求得和及进位的逻辑电路称为全加器。全加器公式:
其中,A、B为两个1位二进制加数,CI为低位来的进位,S为本位的和,CO为本位向高位的进位。
多位加法器
一般有串行进位加法器和超前进位加法器两种。
串行进位加法器
将N位全加器串联起来,低位全加器的进位输出连接到相邻的高位全加器的进位输人,这种进位方式称为串行进位。由于串行进位加法器的进位信号采用逐级传输方式,每一位的加法运算必须在低一位的加法运算完成之后才能进行,故其运算速度慢,只能用于低速数字设备中。但这种电路的结构简单,实现加法的位数扩展方便。
超前进位加法器
超前进位又称并行进位,就是让各级进位信号同时产生,每位的进位只由加数和被加数决定,而不必等低位的进位,即实行了提前进位,因而提高了运算速度。但同时不可避免地,其电路复杂度会随着位数增加而急剧上升。我们日常使用的加法器模块多为超前进位的工作方式,如双全加器74**183、4位超前进位加法器74**283等。
加法器的应用
构成加减乘除运算器
若需求减法运算,只需把减数转成补码,即可把两数相减变换成两数相加的加法运算。至于乘法运算,可以先计算出每一位的本位和以及进位的表达式,再按照表达式画出逻辑图。例:用全加器实现一个2位二进制乘法运算电路。
假设两个2位二进制数和,两者相乘最高为4位,设为,列竖式计算
具体电路实现方式:利用与门实现、、、(当然,如果题目中不允许使用门器件,也可以使用全加器实现
* ),然后利用一个全加器实现,产生的和就是,产生的进位供给高位计算产生;再利用一个全加器实现,产生的和是,产生的进位就是。逻辑电路图如下:[
* ]: 将全加器的CI端接地,则输出CO即为AB。输出S为构成代码转换器
比如常用的8421BCD码和余3码,它们之间的差值固定,因此通过加减这个差值,可以实现这两种编码的转换。构成二-十进制码加法器
例:用4位二进制加法器构成1位8421BCD码十进制加法器。
首先举例分析十进制数的加法和8421BCD4位二进制码加法的差异。
所以电路应由3个部分组成:第一部分进行加数和被加数相加;第二部分产生修正控制信号;第三部分完成加6修正。第一部分和第三部分均由4位加法器实现。第二部分判别信号F,应在4位8421BCD码相加有进位信号CO产生时或者和数在10~15的情况下产生,所以F应为
化简变换为
根据表达式可绘制出逻辑电路图如下
编码器
编码器一般有普通编码器和优先编码器两种。
普通编码器
在普通编码器中,任何时刻只允许输入一个编码有效信号,否则输出将发生混乱。常见的3位二进制编码器又称8线-3线编码器,4位二进制编码器又称16线-4线编码器。此外还有8421BCD码编码器,这是一种二-十进制编码器。不同的编码器要注意其输入端和输出端的引脚是否有小圆圈,输入端有小圆圈代表低电平有效,否则高电平有效,输出端有小圆圈代表输出为反码,否则输出原码。
优先编码器
在优先编码器电路中,允许同时输人两个以上的编码信号。不过在设计优先编码器时已经将所有的输入信号按优先顺序排了队,当几个输入信号同时出现时,只对其中优先权最高的一个进行编码。
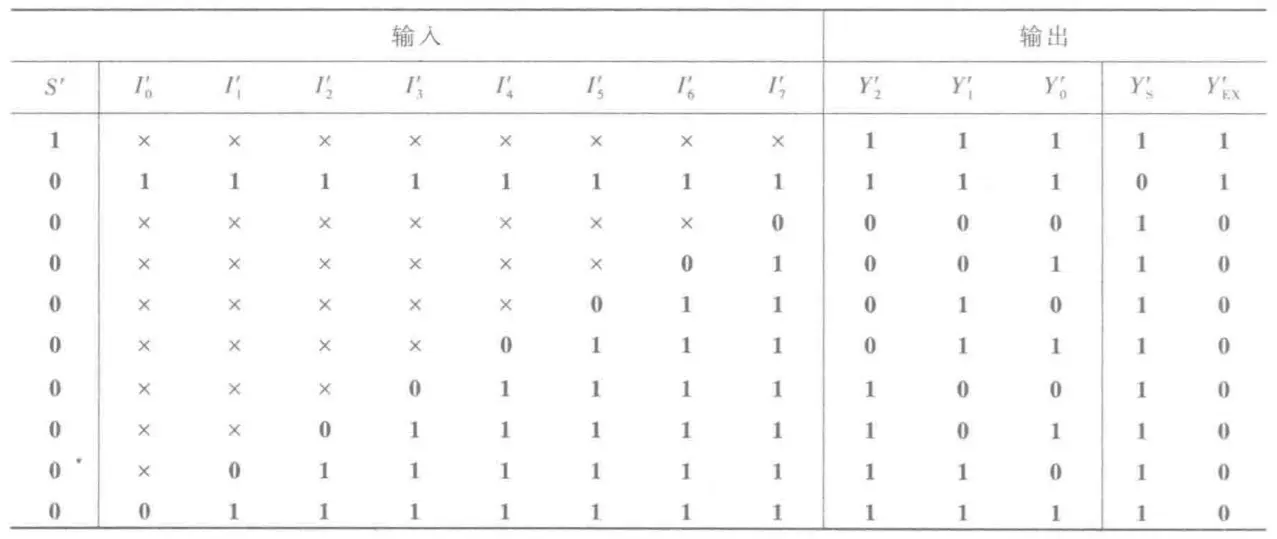
我们常用的有 8线-3线优先编码器74**148,还有 二-十进制优先编码器74**147(输入低电平有效,输出为8421BCD码的反码)。


编码器扩展
例:用8线-3线优先编码器74HC148扩展成16线-4线优先编码器。
显然需要2片74HC148。我们知道74HC148的输出范围为 000 ~ 111,而需要得到的输出为 0000 ~ 1111,不难发现,0000 ~ 1111 可以拆成 0000 ~ 0111 和 1000 ~ 1111 两部分,这两部分的低三位都是 000 ~ 111,不同的只有最高位。我们可以利用使能端和使能输出端,控制其中一片编码器工作,而另一片编码器不工作,而扩展输出端作为输出的最高位。注意,由于74HC148输出为反码,所以低三位输出端用与非门相接。逻辑电路图如下。
译码器
译码是编码的逆过程。译码器的种类很多,根据所完成的逻辑功能可分为变量译码器、码制译码器和显示译码器3种。
变量译码器
常见的变量译码器有 双2线-4线译码器74**139、3线-8线译码器74**138、4线-16线译码器74**154等。
从功能表可以看出,74HC138的输出,所以这种译码器也称最小项译码器。根据这个特性,我们可以用它来输出特定的逻辑函数表达式。
例:用74HC138输出
先将变换成最小项之和的形式,并变换成与非式。
逻辑电路图如下:
码制译码器
最常用的是8421BCD码译码器,即 二-十进制译码器74**42。
根据真值表可见,若将接地,弃用,此时74HC42就可作为一片3线-8线译码器使用。
显示译码器
常用的主要是74**48。
其中,LT' 为灯测试输入,令 LT' = 0 可将所有数码管点亮,已检查发光是否正常。平时应置 LT' 为1。
RBI' 为灭零输入,其功能是把冗余的0熄灭,比如“00013.700”变成“13.7”。
BI'/RBO'为灭灯输入/灭零输出,当作输入端使用时,称灭灯输入控制端,令 BI' = 0 即可熄灭所有数码管;当作为输出端使用时,称灭零输出端,只有当输入 A 全为 0,且 RBI' = 0 时,才有输出 RBO' = 0,表明已经将本来应该显示的零熄灭了。
将 BI'/RBO' 与 RBI' 配合使用,很容易实现多位数码显示的灭零控制。将多谐振荡器与 BI'/RBO' 相连接,还可以实现亮度调节(PWM控制间歇显示)。
译码器扩展
例:用3线-8线译码器74HC138扩展成4线-16线译码器。
例:用2线-4线译码器74LS139和4线-10线译码器74LS42扩展成5线-32线译码器。
数据选择器
数据选择器输出通用表达式:
常见的有 双4选1数据选择器74**153,8选1数据选择器74**151。其中S为选通端,A为地址端。芯片画法不固定,一般标注“MUX”的也是数据选择器。
数据选择器扩展
例:用8选1和4选1数据选择器扩展成32选1数据选择器。
数据选择器生成函数
用具有N个地址端的数据选择器实现M变量逻辑函数(M ≤ N)
- 当 M = N 时,只需将选择器的输入端按照卡诺图中对应的 0 和 1 填写。
例:用8选1数据选择器实现3变量逻辑函数:
显然,,故将接1,而则接0。
- 当 M < N 时,只需要将高位地址端和相应输入端接地(接0)即可。
例:用8选1数据选择器实现2变量逻辑函数:
显然,,故将接1,而则接0,至于地址端,高位接0,剩余。
用具有N个地址端的数据选择器实现M变量逻辑函数(M > N)
- 一种方法是扩展法,一般将最高位作为片选信号。
例:用8选1数据选择器实现4变量逻辑函数:
- 另一种方法是降维图法。
降维的方法是:如果记图变量为,对于原卡诺图(或降维图)中,当 时,原图单元值为 ; 时,原图单元值为 ,则在新的降维图中,对应的降维图单元填入子函数 。其中 和 可以为0,可以为1,可以为某一变量,也可以为某一函数。
例:用8选1数据选择器实现4变量逻辑函数:
降维可得:。绘制出逻辑电路图如下:
数值比较器
数值比较器的输入为要进行比较的两个二进制数,输出为比较的三个结果:大于、小于和等于。
对于1位数值比较器,其逻辑表达式为
在比较两个多位数的大小时,必须自高而低地逐位比较,而且只有在高位相等时,才需要比较低位。常用的集成模块有 4位数值比较器74**85。
数值比较器有串联和并联2种扩展方式,当位数较少且要求速度不高时,常采用串联方式;当位数较多且要满足一定速度要求时,应采用并联方式。
竞争与冒险
理想情况下,在组合逻辑电路的设计中,假设电路的连线和集成门电路都没有延迟,电路中的多个输入信号发生变化时,都是同时瞬间完成的。实际上,信号通过连线及集成门都有一定的延迟时间,输入信号变化也需要一个过渡时间,多个输入信号发生变化时,也可能有先后快慢的差异。因此,在理想情况下设计的组合逻辑电路,受到上述因素的影响后,可能在输入信号发生变化的瞬间,在输出端出现一些不正确的尖峰信号。这些尖峰信号又称毛刺信号,主要是由信号经不同的路径或控制,到达同一点的时间不同而产生的竞争引起的,故称为竞争冒险现象,简称竞争冒险或冒险。它分为静态冒险和动态冒险两大类。
静态冒险分为静态1冒险和静态0冒险两类。静态1冒险,Y=AA';静态0冒险,Y=A+A'。
竞争冒险的判断
代数法
若输出函数在一定条件下可以简化为某原变量与反变量之和或之积,则电路存在竞争冒险现象。
例如F=AB+A'C,当B=C=1时,F=A+A',所以该电路存在竞争冒险现象。卡诺图法
若输出函数的卡诺图上,存在包围圈相邻的情况,则有竞争冒险现象;包围圈相交或不相邻,则无竞争冒险。
竞争冒险的消除
修改逻辑设计
可以通过对输出函数增加冗余项,修改逻辑设计。
例如 F=AB+A'C 添加冗余项 BC 变成 F=AB+A'C+BC。⇨
引入选通脉冲
加输出滤波电容

































 ⇨
⇨
















